
SHA-256 Hashing: A Secure Algorithm for Data Integrity
Written by: Rugved Koshiya | 14 JULY
How to Calculate SHA-256 Hash for Any Data
Have you ever wondered how websites store passwords securely?
Or how you can verify the integrity of a downloaded file?
Or how cryptocurrencies like Bitcoin work?
If you have, then you might have heard of a term called SHA-256 Hashing a secure algorithm.
SHA-256 Hashing a secure algorithm is a process of transforming any given data into another value that is shorter, fixed-length, and unique. Hashing is widely used for encryption, authentication, digital signatures, and other applications that require verifying the identity or integrity of data.
In this blog post, we will explain what SHA-256 Hashing a secure algorithm is, how it works, and how to calculate one of the most popular and secure hashing algorithms: SHA-256. SHA-256 stands for Secure Hash Algorithm 256-bit and it can generate a 256-bit (32-byte) hash value for any data, whether it is text, image, video, audio, or anything else.
What is SHA-256 Hashing ?
Hashing is a mathematical function that takes any input data and produces an output value called a hash or a digest. The hash value has the following properties:
- It is much shorter than the input data. For example, SHA-256 can produce a 256-bit hash value for any input data, no matter how large or small it is.
- It is unique for each input data. This means that if you change even one bit of the input data, the hash value will change completely. This property is also called the avalanche effect.
- It is irreversible. This means that you cannot recover the input data from the hash value. This property makes hashing suitable for encryption and password protection.
Hashing is different from encryption in that encryption is reversible (you can decrypt the encrypted data with the right key) and encryption usually produces an output value that is similar in size to the input data.
How Does Hashing Work?
Hashing works by applying a series of mathematical operations to the input data. These operations are designed to be fast, deterministic, and unpredictable. There are many different hashing algorithms, each with its own set of operations and rules.
One of the most widely used hashing algorithms is SHA-256. SHA-256 belongs to a family of hashing algorithms called SHA-2, which was developed by the US National Security Agency (NSA) in 2001. SHA-256 is considered to be very secure and resistant to attacks.
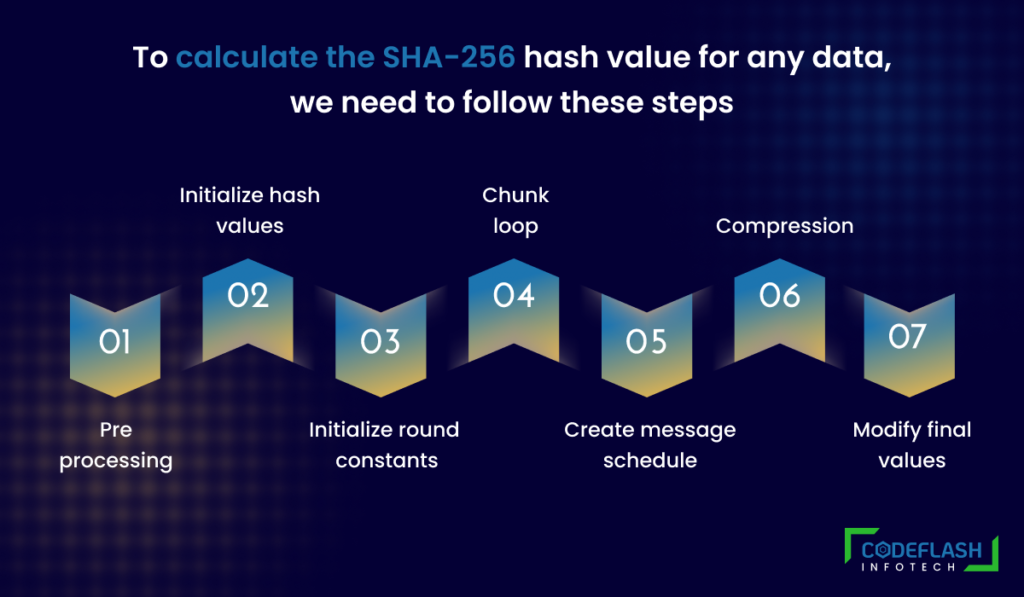
To calculate the SHA-256 Hashing a secure algorithm value for any data, we need to follow these steps:
- Pre-processing: Convert the input data into binary format (a sequence of 0s and 1s) and pad it with some extra bits to make it a multiple of 512 bits. The padding consists of adding a 1 bit followed by as many 0 bits as needed and then adding a 64-bit number that represents the length of the original input data in bits.
- Initialize hash values: Set up eight variables (h0, h1, h2, h3, h4, h5, h6, h7) with some initial values that are derived from the square roots of the first eight prime numbers.
- Initialize round constants: Set up 64 constants (k0, k1,… k63) that are derived from the cube roots of the first 64 prime numbers.
- Chunk loop: Divide the padded input data into chunks of 512 bits each and process each chunk one by one.
- Create message schedule: Divide each chunk into 16 words of 32 bits each and then expand them into 64 words by applying some bitwise operations.
- Compression: For each word in the message schedule, perform some bitwise operations that involve the eight hash values and the round constants and update the hash values accordingly.
- Modify final values: After processing all the chunks, add the final hash values together to get the final SHA-256 hash value.
How to Calculate SHA-256 Hash for "hello world"
Step 1: Pre-Processing
- In this step this algorithm generally takes binary value from data file weather it is string, audio, video, etc…
- All data stored in computers, or any other electronic devices are in binary.
- So let’s calculate ASCII value from
hello worldthen we get binary value from it.
| Character | Decimal | Binary |
|---|---|---|
| h | 104 | 01101000 |
| e | 101 | 01100101 |
| l | 108 | 01101100 |
| l | 108 | 01101100 |
| o | 111 | 01101111 |
| (space) | 32 | 00100000 |
| w | 119 | 01110111 |
| o | 111 | 01101111 |
| r | 114 | 01110010 |
| l | 108 | 01101100 |
| d | 100 | 01100100 |
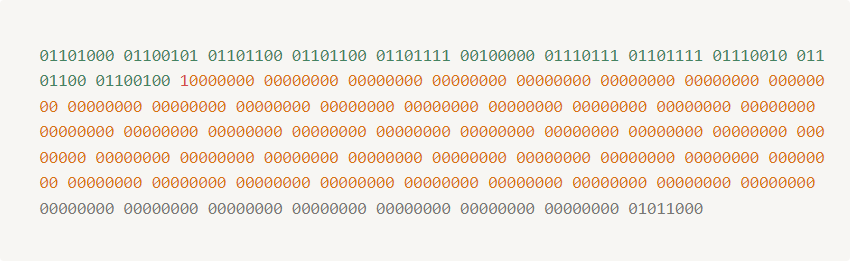
- So the final binary value is here by concatenating each.

- The length of our data is
88 bits - Here in this algorithm a chunk is of
512 bits. At this step we reserve64 bitsfrom512 bitsfor future use. - So, $512 \space bits – 64 \space bits = 488 \space bits$
A chunk is a fragment of information.
Lets suppose we are having 2MB of data so we can divide it into 4 part of 512 KB so each 512 KB block called chunk.
- Now, our data is 88 bits and chunk size is 512-64 = 488 bits so we have to expand our data to complete 448 bits.
- So we add one
1and append all0until it’s length reaches to488. - Our resultant data in bits representation is below:

- So our data chunk is now
448 bitsso now to make it512 bitswe add64 bitsto it. Now question is what we will add for 64 bits? - We know our actual data size is
88 bitswhose binary representation is01011000. so we add this as64bitbinary. - Our resultant data is as below:
Step 2: Initialize Hash Values (h)
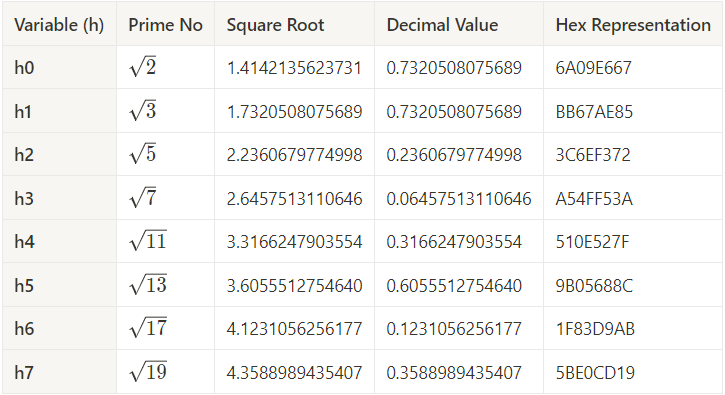
- In this step we will initialize
8default hash value we call them name withh0,h1,h2,h3,h4,h5,h6,h7. - First 8 prime numbers are:
2, 3, 5, 7, 11, 13, 17, 19 - So we calculate
square rootof prime numbers and assign its fractional part toh0 → h7
Step 3: Initialize Round Constants (k)
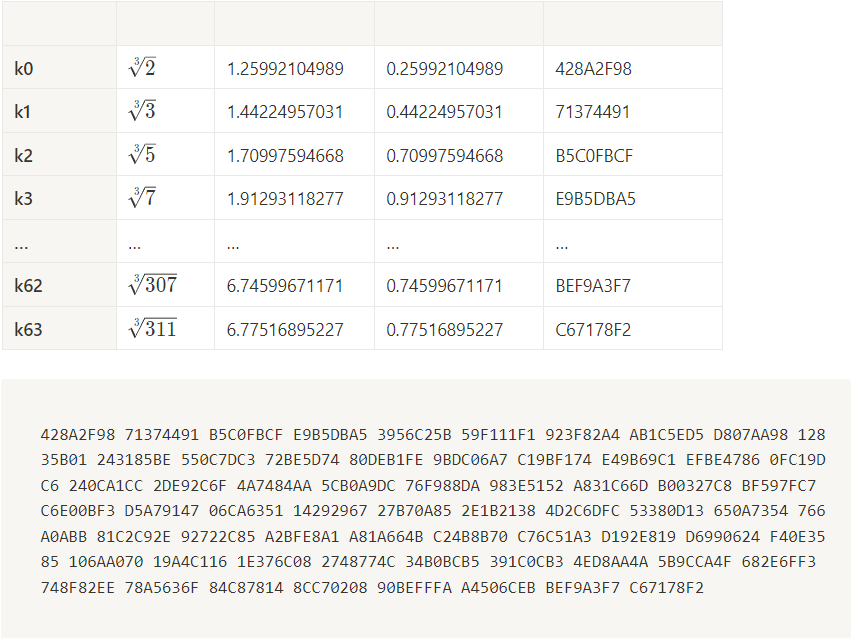
- In this step we will initialize
64constant we call them name withk. - First 64 prime numbers are (2→311):
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311 - So we calculate
cube rootof prime numbers and assign its fractional part tok0 → k63
Step 4: Chunk Loop
- The following steps will happen for each
512-bit chunkof data from our input. In our case, becausehello worldis so short, we only have one chunk. At each iteration of the loop, we will be mutating the hash valuesh0 - h7which will be the final output.
Step 5: Create Message Schedule (w)
- Now below is our data in
8 bitbinary format

- We will now convert it into
32 bit binaryso it will look something like below:

- So our actual data is now of
16 bitsof32bitsso for completing64 bitsblock we required $64 \space bits – 16 \space bits = 48 \space bits$ - So we append all
0in 32 bit representation in order to complete 64 bits. - So our data is now as below:

Now we apply one formula and modify this appended 0 to increase complexity and it make sure that the hash value is not dependent on any single bit. If one bits gets change all hash value changes.
Algorithm
- Modify the zero-ed indexes at the end of the array using the following algorithm:

- Let’s do for
w[16]so we can see how it works

- By following above mathematical operations for all we get result as shown below:

Step 6: Compression
- In this step we compress our message schedule data block.
- Initialize variables a, b, c, d, e, f, g, h and set them equal to the current hash values respectively h0, h1, h2, h3, h4, h5, h6, h7
- We run a some mathematical operation for each bit presented in
64 bit message scheduling block

- By doing above iteration for
64 timeswe get value ofa → his given below :
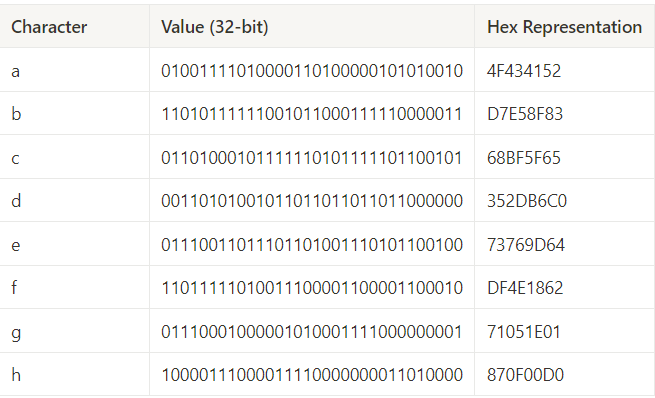
- Value from
h0 → h7is given below:

Step 7: Modify Final Values
- After the compression loop, but still, within the chunk loop, we modify the hash values by adding their respective variables to them.
- Below table is is having function of updating
h0 → h7values.

- In our case we have only 1 chunk so our all mathematical operation is complete here else if there is more chunks then we update
h0 → h7and then repeat for next chunk with new updatedh0 → h7values.
Step 8: Concatenate Final Hash
Hash value = h0 append h1 append h2 append h3 append h4 append h5 append h6 append h7
Hash value = B94D27B9 append 934D3E08 append A52E52D7 append DA7DABFA append C484EFE3 append 7A5380EE append 9088F7AC append E2EFCDE9
Hash value = B94D27B9934D3E08A52E52D7DA7DABFAC484EFE37A5380EE9088F7ACE2EFCDE9
Our final SHA-256 hash for hello world is
B94D27B9934D3E08A52E52D7DA7DABFAC484EFE37A5380EE9088F7ACE2EFCDE9




